Bifurcations and nonlinearity with macromolecules
Typical enzymes are roughly spherical nanoparticles of size ∼ 4 nm, consisting of ∼ 2000 atoms; a 30 base pair DNA molecule is roughly a cylinder 10 nm long and 2 nm in diameter, also consisting of about 2000 atoms. Such compact macromolecules display unusual mechanical properties which are mostly not well characterized. They are interesting materials.
Consider, for example, that the individual molecule is a "self-healing" chunk of matter which can "fracture" and re-assemble reversibly when driven beyond the linear elasticity regime. Large nonlinearities can coexist with reversible mechanical behavior: a property which may be necessary for a nano-machine.
One interesting case is provided by short DNA molecules. Double stranded DNA has been recently used as a "molecular spring" to mechanically perturb the conformation of enzymes, and therefore mechanically control a variety of chemical reactions. We are thus interested in characterizing quantitatively the mechanics of the DNA springs. The relevant regime is the nonlinear one of sharp bending of the DNA. As a polymer physics problem, we ask: is it possible to "replace" the complex chemical structure of the molecule with a small number of effective parameters as far as the mechanical properties are concerned?
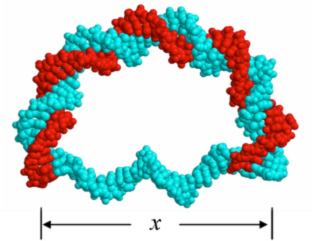
Figure 1 at left: this DNA molecule stores a large elastic energy, resulting from the bending of the ds (upper) part and stretching of the ss (lower) part).
We address this question with the stressed molecule shown in Fig. 1, where the ds DNA part (red & blue) is bent and the ss part (blue) is stretched. We measure the elastic energy of this molecule by a thermodynamics method invented in the lab. An example is shown in Figure 2. Increasing the number of bases Ns in the ss part of the molecule has the effect of increasing x (the end-to-end distance of the ds part of the molecule). Measuring the elastic energy for varying Ns is then equivalent to measuring for varying x. The interesting nonlinearity evident in the measurements is described here [Qu 2011a]. It corresponds to the formation of a (reversible) kink in the ds DNA. It turns out that the bending elasticity of this complex molecule is captured by just two effective parameters: a bending modulus (previously known) and a critical bending torque (which we determined with these experiments). An analytically solvable model based on these two parameters describes the whole energy function, from low energies to high energies (that is, in the linear and the nonlinear regimes), within a fraction of 1 kT (red curve in Fig. 2).
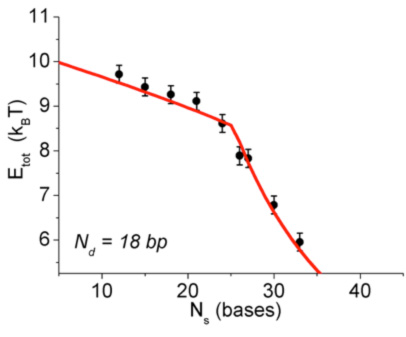
Figure 2 at right: The total elastic energy measured for the stressed molecule of Fig. 1, for varying Ns (number of bases in the ss part), at fixed Nd = 18 (number of bp in the ds part). The "knee" in the curve corresponds to the appearance of a kink in the ds DNA. The line is a fit using an analytically solvable model for the bending energy of ds DNA. The model introduces a new materials parameter in the physics of DNA: the critical bending torque at which the molecule develops a kink.
Mechanical nonlinearity in an ion channel. Voltage gated ion channels enable electrical signal propagation along neurons. These transmembrane proteins operate by coupling the motion of a charged group of aminoacids (the "gate") to the opening of a pore permeable to ions. The motion of the gate is driven by the electric field across the cell membrane. It is relatively easy to mechanically drive these channels in an artificial supported bilayer setup. In the lab, we perform what are essentially rheology experiments on a model voltage gated potassium channel (the KvAP). We shake the gate through an AC electric field and observe the ionic current. We find an essential nonlinearity in the response, where the current saturates and even decreases for increasing voltage.
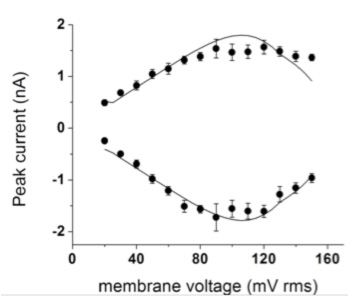
Figure 3 at left: Ionic current (from multi-channel recordings) measured while driving the channels with an AC voltage at 100 Hz. Both the positive and negative peak currents are shown, vs amplitude of the voltage. The curves are nonlinear in the driving amplitude: the peak current saturates and even decreases as the voltage is increased. The solid lines represent a mechanically coupled, nonlinear model.
This behavior must originate in a variable phase lag between the motions of the gate and the pore. A simple mechanical model leads to a force dependent internal viscosity for the conformational motion of the channel. In essence, the harder you squeeze it, the stiffer the molecule becomes.
The picture which emerges is that when it comes to dynamics, these molecules with their beautifully complex structure are neither solid nor liquid but rather resemble “silly putty” in their mechanical response.
Softening transition of enzymes. Enzymes are compact but mechanically soft macromolecules. They are reversibly deformed by an applied static or dynamic stress. With this experiment we find that, beyond a few Angstrom deformation, an enzyme undergoes a softening transition. The equilibrium mechanical response of the enzyme is that of a nonlinear spring with a (reversible) yield point.
The measurements are obtained using a system of two mechanically coupled biomolecules: the enzyme (a L uciferase in this case) and a DNA “spring”. The enzyme is deformed by the action of the DNA spring; similar enzyme – DNA chimeras allow to probe the mechanics of other enzymes also. We examine the response of the enzyme for different states of stress. We find that small changes in the stress cause large changes in activity. This nonlinear behavior is qualitatively interpreted as arising from a soft regime of the enzyme beyond linear elasticity. In the case of the (Renilla) Luciferase we find a restoring force of the molecule in the soft regime of approximately 4 pN.
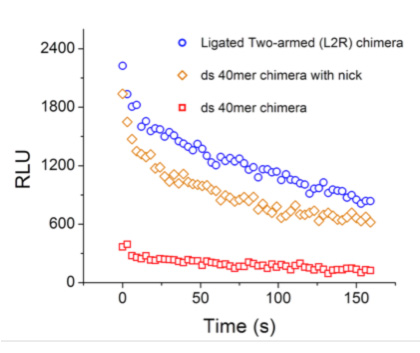
This is similar to the forces produced by motor proteins, which suggests that motors also may be operating in a similar soft (or “relaxational”) mechanical regime of the structure. We believe that this soft regime enables large conformational motion in enzymes. Indeed, the equilibrium softening transition suggested by these measurements mirrors a corresponding nonequilibrium transition seen in the nano-rheology experiments (see the project: Viscoelastic Enzyme), and may be a universal feature of the mechanics of compact biomolecules.
Figure 4 at left: Modulation of enzymatic activity of Renilla Luciferase under mechanical stress. Plotted is the light intensity emitted (proportional to reaction speed) in the course of time. Circles: no stress; diamonds: small stress; squares: larger stress.
Associated publications:
- H. Qu, C-Y. Tseng, Y. Wang, A. J. Levine, and G. Zocchi, "The elastic energy of sharply bent nicked DNA," Europhys. Lett. 90, 18003 (2010).
- Hao Qu and Giovanni Zocchi, “The complete bending energy function for nicked DNA”, Europhys. Lett. 94, 18003 (2011a)
- H. Qu, Y. Wang, C-Y. Tseng, and G. Zocchi, “Critical torque for kink formation in double stranded DNA”, Phys. Rev. X 1, 021008 (2011).
- A. Ariyaratne and G. Zocchi, “Nonlinearity of a voltage gated potassium channel revealed by the mechanical susceptibility”, Phys. Rev. X 3, 011010 (2013).
- C-Y. Tseng and G. Zocchi, “Equilibrium softening of an enzyme explored with the DNA spring”, Appl. Phys. Lett. 104, 153702 (2014).